
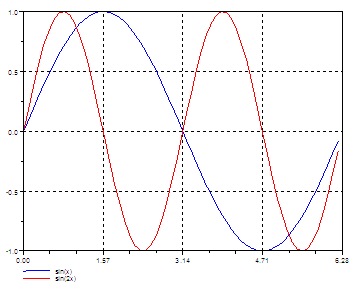

A collection collection of finite difference formulas formulas. Accuracy Accurac y of finite difference formulas formulas. A three three points points formula formula for for the second second deriv derivati ative ve. Somee finite differen Som difference ce formula formulass for the first derivati derivative ve. Centere Cen tered d form formula ula wit with h 4 poin points ts. Centere Cen tered d form formula ula wit with h 2 poin points ts. Numerical Numeri cal experimen experiments ts with with the robust robust forwa forward rd formula formula. Floating Floati ng point point implemen implementation tation of the forwa forward rd formula formula. 64 Vari arious ous resu results lts for sin sin(2 (2 ). 2 Fin Finite ite diff differen erences ces. 2.1.1 Tayl aylor’s or’s form formula ula for univ univariate ariate functio functions ns 2.1.2 2.1. Ģ A surp surpri risi sing ng res resul ultt In the the thir third d part, part, we pres presen entt the the derivative function function, its featur features es and its performances. We presen presentt severa severall formula formulass and their their associa associated ted optima optimall steps. In the second part, we analyse the method to use the optimal step to compute derivatives with finite differences on floating point system systems. In the first part, we present a result which is surprising when we are not familiar with floating point numbers. This approach was designed for first year students from all engineering degrees that have electronics/electricity courses in their curricula.Numerical Derivatives in Scilab Micha¨el el Baudin May 2009 Abstract This document document present present the use of numerical numerical derivativ derivatives es in Scilab.
#Scilab derivative software#
The students can use the toolbox through the web platform (in computers where they doesn't have installation privileges) or in is personal computer by installing both the SCILAB software and the toolbox. The toolbox runs entirely in the Moodle web platform and provides the same results as the standalone application. The developed tool was based on the numerical analysis software SCILAB and is a toolbox that gives their users the opportunity to obtain the end results of a circuits analysis but also the expressions obtained when derivative and integrals calculations are necessary, plot signals, obtain vector diagrams, etc. Also, they are not very effective in obtaining graphical results that could be used to elaborate reports and for an overall better comprehension of the results. By the most part, in electronic circuit analysis, it is necessary to solve linear equation systems with 3 or more variables (sometimes in the complex domain) and solve numerical derivatives and integrals.įurthermore, graphical results are a big part of electronics courses since it is often necessary to sketch a plot of the output signal (capacitor charge/discharge, diodes, etc), obtain vector diagrams (transient analysis) and Bode plots (frequency analysis).Īnalyzing the existing circuit simulators software tools, it is clear that even though they are very helpful by showing the end result they are not so effective in the process of the students studying and self learning since they show results but not intermediate steps which are crucial in problems that involve derivatives or integrals.
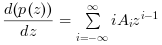
The first approach was to assess the mathematical skill necessary to solve all the problems related to electronics and electricity courses. The toolbox was developed to be used as standalone or integrated in an e-learning platform. Nonetheless, any other equivalent software could be used such as Matlab or Octave. This allows students and institutions to use toolbox without any financial burden. The growing acknowledgment and acceptance of open source software lead to the choice of an open source software tool – SCILAB, which is a numerical analysis tool – to develop a toolbox. In this paper a software tool to be used by first year students in electronics/electricity courses is presented.
#Scilab derivative how to#
One of the main problems with using these tools is when and how to start use them so that they can be beneficial to students and not mere substitutes for potentially difficult calculations or design. electronic circuits), computer assisted design tools and others, depending on the degree. Engineering graduates are familiar with numerical analysis tools but also in simulators (e.g. Engineering courses lead the way in this development and these tools became almost a standard. Software tools in education became popular since the widespread of personal computers.


 0 kommentar(er)
0 kommentar(er)
